Разделы: Физика

Постановка задачи: Мы уже много знаем о механических колебаниях: свободные и вынужденные колебания, автоколебания, резонанс и т.д. Приступаем к изучению электрических колебаний. Тема сегодняшнего урока: получение свободных электромагнитных колебаний.

Вспомним вначале: Каким условиям должна соответствовать колебательная система, система, в которой могут возникать свободные колебания. Ответ: в колебательной системе должна возникать возвращающая сила и происходить превращение энергии из одного вида в другой.

(Разбор нового материала по презентации с подробным пояснением всех процессов и записью в тетради первых двух четвертей периода, 3 и 4-ые четверти описать дома, по образцу).

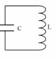
Колебательный контур – это электрическая цепь, в которой можно получить свободные электромагнитные колебания. К.К. состоит всего из двух приборов: катушки индуктивностью L и конденсатора электроёмкостью С. Идеальный колебательный контур не имеет сопротивления.

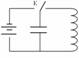
Чтобы сообщить энергию в К.К., т.е. вывести его из положения равновесия, нужно временно разомкнуть его цепь и поставить ключ с двумя положениями. Когда ключ замкнут на источник тока, то конденсатор заряжается до максимального заряда. Этим подают в К.К. энергию в виде энергии электрического поля. Когда ключ замкнут в правое положение, то источник тока отключен, К.К. предоставлен самому себе.

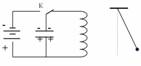
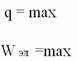
Такое состояние К.К. соответствует положению математического маятника в крайнем правом положении, когда его вывели из состояния покоя. Колебательный контур выведен из положения равновесия Заряд конденсатора – максимален и энергия заряженного конденсатора – энергия электрического поля максимальна. Будем рассматривать весь процесс, который происходит в нём по четвертям периода.

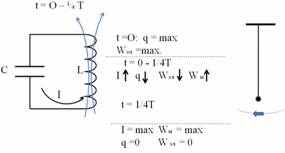
В 1-ый момент конденсатор заряжен до максимального заряда (нижняя обкладка заряжена положительно), энергия в нём сосредоточена в виде энергии электрического поля. Конденсатор замкнут сам на себя, и он начинает разряжаться. Положительные заряды по закону Кулона притягиваются к отрицательным, и возникает ток разрядки, направленный против часовой стрелки. Если бы на пути тока не было бы катушки индуктивности, то всё произошло бы мгновенно: конденсатор бы просто разрядился. Накопленные заряды компенсировали бы друг друга, энергия электрическая превратилась бы в тепловую. Но в катушке возникает магнитное поле, направление которого можно определить по правилу буравчика – «вверх». Магнитное поле – растущее и возникает явление самоиндукции, которое препятствует росту тока в нём. Ток растёт не мгновенно, а постепенно, в течение всей 1-ой четверти периода. За это время ток будет расти до тех пор, пока его поддерживает конденсатор. Как только конденсатор разрядится, ток больше не растёт, он к этому моменту достигнет максимального значения. Конденсатор разрядился, заряд равен 0, значит и энергия электрического поля равна 0. Но в катушке течёт максимальный ток, вокруг катушки существует магнитное поле, значит, произошло превращение энергии электрического поля в энергию магнитного поля. К концу 1-ой четверти периода в К.К.ток максимальный, энергия сосредоточена в катушке в виде энергии магнитного поля. Это соответствует, тому положению маятника, когда он проходит положение равновесия.

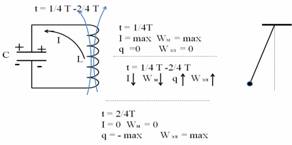
В начале 2-ой четверти периода, конденсатор разряжен, а ток достиг максимального значения и он должен был бы мгновенно исчезнуть, ведь конденсатор его не поддерживает. И ток действительно начинает резко убывать, но он течёт по катушке, и в ней возникает явление самоиндукции, которое препятствует любому изменению магнитного поля, вызывающего это явление. ЭДС самоиндукции поддерживает исчезающее магнитное поле, индукционный ток имеет то же направление, что и существующий. В К.К. ток течёт против часовой стрелки – в пустой конденсатор. В конденсаторе накапливается электрический заряд – на верхней обкладке – положительный заряд. Ток течёт до тех пор, пока его поддерживает магнитное поле, до конца 2-ой четверти периода. Конденсатор зарядится до максимального заряда (если не произойдёт утечки энергии), но противоположного направления. Говорят, конденсатор перезарядился. К концу 2-ой четверти периода ток исчезает, значит, энергия магнитного поля равна 0.Конденсатор перезарядился, его заряд равен ( – максимальному). Энергия сосредоточена в виде энергии электрического поля. В течение этой четверти произошло превращение энергии магнитного поля в энергию электрического поля. Состояние колебательного контура соответствует такому положению маятника, при котором он отклоняется в крайнее левое положение.

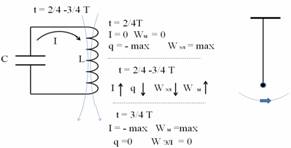
В 3-ей четверти периода происходит всё также, что и в 1-ой четверти, только противоположного направления. Конденсатор начинает разряжаться. Ток разрядки растёт постепенно, в течение всей четверти, т.к. быстрому росту его препятствует явление самоиндукции. Ток растёт до максимальной величины, пока конденсатор не разрядится. К концу 3-ей четверти энергия электрического поля превратится в энергию магнитного поля, полностью, если не будет утечки. Это соответствует такому положению маятника, когда он снова проходит положение равновесия, но в противоположном направлении.

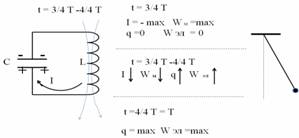
В 4-ой четверти периода происходит всё так же, как и во 2-ой четверти, только в противоположном направлении. Ток, поддерживаемый магнитным полем, постепенно убывает, поддерживаемый ЭДС самоиндукции и перезаряжает конденсатор, т.е. возвращает его к первоначальному положению. Энергия магнитного поля превращается в энергию электрического поля. Что соответствует возвращению математического маятника в первоначальное положение.

Анализ рассмотренного материала:

1. Можно ли колебательный контур рассматривать, как колебательную систему? Ответ: 1. В колебательном контуре происходит превращение энергии электрического поля в энергию магнитного поля и наоборот. 2. Явление самоиндукции играет роль возвращающей силы. Поэтому колебательный контур рассматривать, как колебательную систему. 3. Колебания в К.К. можно считать свободными.

2. Можно ли колебания в К.К. рассматривать, как гармонические? Анализируем изменение величины и знака заряда на обкладках конденсатора и мгновенного значения тока и его направления в цепи.

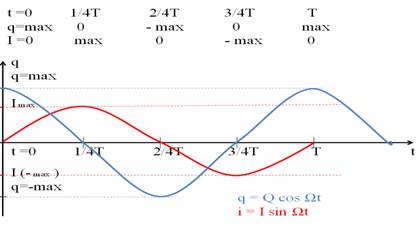
На графике видно:

1. Заряд и сила тока изменяются по гармоническому закону, и мы можем записать соответствующие законы.
2. Фазы колебаний тока и заряда не совпадают. Заряд опережает ток по фазе на 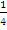периода.

3. Что в колебательном контуре колеблется? Какие физические тела совершают колебательные движения? Ответ: колеблются электроны, они совершают свободные колебания.

4. Какие физические величины изменяются при работе колебательного контура? Ответ: изменяются сила тока в цепи, заряд в конденсаторе, напряжение на обкладках конденсатора, энергия электрического поля и энергия магнитного поля.

5. Период колебаний в колебательном контуре зависит только от индуктивности катушки L и ёмкости конденсатора C. Формула Томсона: Т = 2π 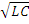можно сравнить и с формулами для механических колебаний.

5.1 Идеальный колебательный контур.

Колебательный контур называется идеальным, если он состоит из катушки и емкости и в нем нет сопротивления потерь.

Р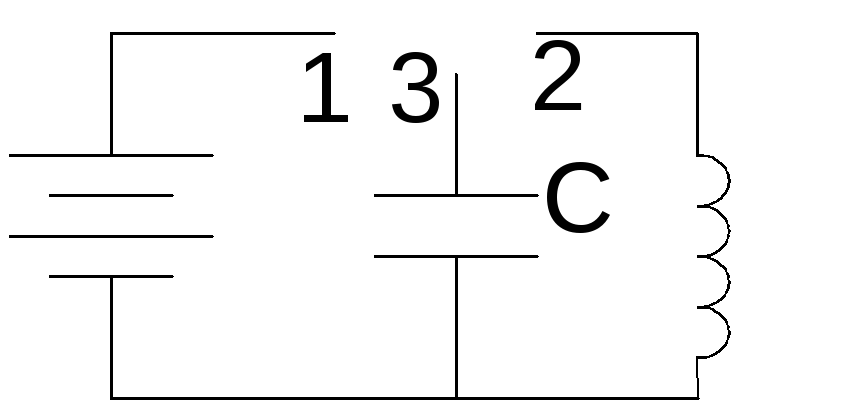ассмотрим физические процессы в следующей цепи:

1 Ключ стоит в положении 1. Конденсатор начинает заряжаться, от источника напряжения и в нем накапливается энергия электрического поля,

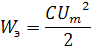
т.е.конденсатор становится источником электрической энергии.

2. Ключ в положении 2. Конденсатор начнет разряжаться. Электрическая энергия, запасенная в конденсаторе переходит в энергию магнитного поля катушки.

Ток в цепи достигает максимального значения(точка 1). Напряжение на обкладках конденсатора уменьшается до нуля.

В период от точки 1 до точки 2 ток в контуре уменьшается до нуля, но как только он начинает уменьшатся , то уменьшается магнитное поле катушки и в катушке индуцируется ЭДС самоиндукции, который противодействует уменьшению тока, поэтому он уменьшается до нуля не скачкообразно, а плавно. Так как возникает ЭДС самоиндукции, то катушка становится источником энергии. От этой ЭДС конденсатор начинает заряжаться, но с обратной полярностью (напряжение конденсатора отрицательное) (в точке 2 конденсатор вновь заряжается).

Вывод: в цепи LC происходит непрерывное колебание энергии между электрическим и магнитным полями, поэтому такая цепь называется колебательным контуром.

Получившиеся колебания называются свободнымиилисобственными, поскольку они происходят без помощи постороннего источника электрической энергии, внесенной ранее в контур (в электрическое поле конденсатора). Так как емкость и индуктивность идеальны (нет сопротивления потерь) и энергия из цепи не уходит, амплитуда колебаний с течением времени не меняется и колебания будут незатухающими.

Определим угловую частоту свободных колебаний:

Используем равенство энергий электрического и магнитного полей

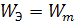
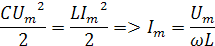
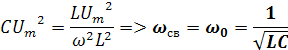
,где ώ угловая частота свободных колебаний.

Период свободных колебаний Т0=1/f.

Частоту свободных колебаний называют частотой собственных колебаний контура.

Из выражения: ώ²LC=1получимώL=1/Cώ, следовательно, при токе в контуре с частотой свободных колебаний индуктивное сопротивление равно емкостному сопротивлению.

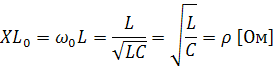
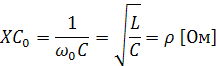
Индуктивное или емкостное сопротивление в колебательном контуре при частоте свободных колебаний называется характеристическим сопротивлением.

Характеристическое сопротивление вычисляется по формулам:

5.2 Реальный колебательный контур

Реальный колебательный контур обладает активным сопротивлением, поэтому при воздействии в контуре свободных колебаний энергия предварительно заряженного конденсатора постепенно тратится, преобразуясь в тепловую.

Свободные колебания в контуре являются затухающими, так как в каждый период энергия уменьшается и амплитуда колебаний в каждый период будет уменьшаться.

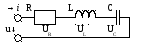
Рисунок – реальный колебательный контур.

Угловая частота свободных колебаний в реальном колебательном контуре :

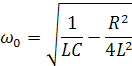
Если R=2… , то угловая частота равна нулю, следовательно свободные колебания в контуре не возникнут.

Таким образом колебательным контуромназывается электрическая цепь состоящая из индуктивности и емкости и обладающая малым активным сопротивлением, меньшим удвоенного характеристического сопротивления, что обеспечивает обмен энергией между индуктивностью и емкостью.

В реальном колебательном контуре свободные колебания затухают тем быстрее, чем больше активное сопротивление.

Для характеристики интенсивности затухания свободных колебаний используется понятие «затухание контура» – отношение активного сопротивления к характеристическому.

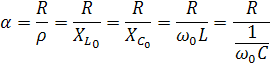
На практике используют величину, обратную затуханию – добротность контура.

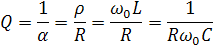
Для получения незатухающих колебаний в реальном колебательном контуре необходимо в течение каждого периода колебаний пополнять электрическую энергию на активном сопротивлении контура в такт с частотой собственных колебаний. Это осуществляется с помощью генератора.

Если подключить колебательный контур к генератору переменного тока, частота которого отличается от частоты свободных колебаний контура, то в цепи протекает ток с частотой равной частоте напряжения генератора. Эти колебания называют вынужденным.

Если частота генератора отличается от собственной частоты контура, то такой колебательный контур является ненастроенным относительно частоты внешнего воздействия, если же частоты совпадают, то настроенным.

Задача: Определить индуктивность , угловую частоту контура, характеристическое сопротивление, если емкость колебательного контура 100 пФ, частота свободных колебаний 1,59 МГц.

Добротность колебательного контура определяется по формуле:

Отношение активного сопротивления к характеристическому

Величина обратная затуханию

Какие колебания называются свободными

непрерывные колебания энергии между электрическим и магнитным полями

колебания, амплитуда которых в каждый период времени уменьшается

Тема занятия 8: РЕЗОНАНС НАПРЯЖЕНИЙ

Резонанс напряжений – явление возрастания напряжений на реактивных элементах, превышающих напряжение на зажимах цепи при максимальном токе в цепи, которое совпадает по фазе с входным напряжением.

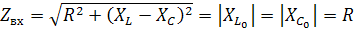
Условия возникновения резонанса:

Последовательное соединение LиCс генератором переменного тока;

Частота генератора должна быть равна частоте собственных колебаний контура , при этом характеристические сопротивления равны;

Сопротивление должно быть меньше, чем 2ρ, так как только в этом случае в цепи возникнут свободные колебания, поддерживаемые внешним источником.

Полное сопротивление цепи:

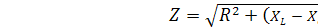=R,

так как равны характеристические сопротивления. Следовательно, при резонансе цепь носит чисто активный характер, значит, входное напряжение, и ток в момент резонанса совпадают по фазе. Ток принимает максимальное значение.

При максимальном значении тока напряжение на участках L и C будут большими и равными между собой.

Напряжение на зажимах цепи:

.

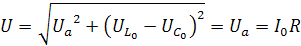Рассмотрим следующие соотношения:

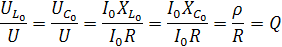, следовательно

.

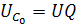Q –добротность контура –при резонансе напряжения показывает, во сколько раз напряжение на реактивных элементах больше входного напряжения генератора, питающего цепь. При резонансе коэффициент передачи последовательного колебательного контура

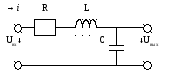
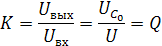
Если добротность равна 100, напряжение на зажимах 1В, то

то есть напряжение на зажимах меньше напряжений на емкости и индуктивности. Это явление называется резонансом напряжений

При резонансе, коэффициент передачи равен добротности.

Построим векторную диаграмму напряжения

Напряжение на емкости равно напряжению на индуктивности, следовательно напряжение на сопротивлении равно напряжению на зажимах и совпадает по фазе с током.

Рассмотрим энергетический процесс в колебательном контуре:

В цепи имеется обмен энергии между электрическим полем конденсатора и магнитным полем катушки. К генератору энергия катушки не возвращается. От генератора в цепь поступает такое количество энергии, которое тратится на резисторе. Это необходимо для того, чтобы в контуре наблюдались незатухающие колебания. Мощность в цепи только активная.

Докажем это математически:

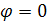
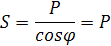, полная мощность цепи, которая равна активной мощности.

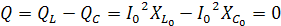, реактивная мощность.

8.1 Резонансная частота. Расстройка.

В цепи, содержащей реактивные элементы, произойдет резонанс, если цепь имеет резистивный характер:

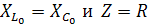
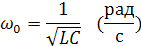
, угловая резонансная частота.

Из формулы видно, что резонанс наступает, если частота питающего генератора равна собственным колебаниям контура.

При работе с колебательным контуром необходимо знать, совпадает ли частота генератора и частота собственных колебаний контура. Если частоты совпадают, то контур остается настроенным в резонанс, если не совпадает – то в контуреприсутствует расстройка.

Настроить колебательный контур в резонанс можно тремя способами:

1 Изменять частоту генератора , при значениях емкости и индуктивности const, то есть изменяя частоту генератора мы подстраиваем эту частоту под частоту колебательного контура

2 Изменять индуктивность катушки, при частоте питания и емкости const;

3 Изменять емкость конденсатора , при частоте питания и индуктивности const.

Во втором и третьем способе изменяя частоту собственных колебаний контура, подстраиваем ее под частоту генератора.

При ненастроенном контуре частота генератора и контура не равны, то есть присутствует расстройка.

Расстройка – отклонение частоты от резонансной частоты.

Существует три вида расстройки:

Абсолютная – разность между данной частотой и резонансной

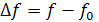
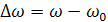
Обобщенная – отношение реактивного сопротивления к активному:

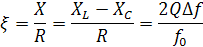
Относительная – отношение абсолютной расстройки к резонансной частоте:

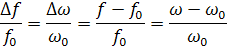
При резонансе все расстройки равны нулю, если частота генератора меньше частоты контура, то расстройка считается отрицательной,

Если больше – положительной.

Таким образом добротность характеризует качество контура, а обобщенная расстройка- удаленность от резонансной частоты.

Сопротивление контура 15 Ом, индуктивность 636 мкГн, Емкость 600 пФ, напряжение питающей сети 1,8 В. Найти собственную частоту контура, затухание контура, характеристическое сопротивление, ток, активную мощность, добротность, напряжение на зажимах контура.

Напряжение на зажимах генератора 1 В, частота питающей сети 1 МГц, добротность 100, емкость 100 пФ. Найти: затухание, характеристическое сопротивление, активное сопротивление, индуктивность, частоту контура, ток, мощность, напряжения на емкости и индуктивности.

Отношение реактивного сопротивления к активному это :

А) Абсолютная расстройка;

Б) Обобщенная расстройка;

В) Относительная расстройка.

Тема занятия 9 : Входные и передаточные АЧХ и ФЧХ последовательного колебательного контура.

9.1 Входные АЧХ и ФЧХ.

В последовательном колебательном контуре:

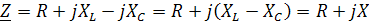, где

R – активное сопротивление;

X – реактивное сопротивление.

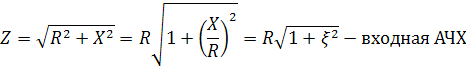
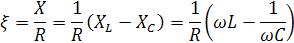,то

ώ=ώ۪۪ζ=0 Z=R

ώ=∞ ζ=∞ Z=∞, следовательно график имеет вид:

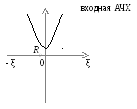
Из графика видно, что контур обладает наименьшим сопротивлением на резонансной частоте, при увеличении расстройки сопротивление увеличивается.

ζ=0 φ=0 R

ФЧХ имеет линейный

характер.

На участке ζ=[-∞;0] – цепь носит активно-емкостной характер;

На участке ζ=[0;∞]- цепь носит frnbdyj-индуктивный характер;

При ζ=0 – цепь носит активный характер;

Передаточные АЧХ и ФЧХ

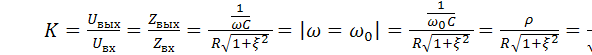
передаточная характеристика АЧХ

ζ=-∞ k=0

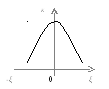ζ=∞ k=0

Построим график зависимости:

Разделим k∕kои получим передаточную

характеристику АЧХ в относительных

единицах, которая имеет вид:

Чтобы построить передаточную ФЧХ необходимо: построить входную ФЧХ, взять её зеркальное ее отображение и сместить на -90°.

Процессы в колебательном контуре

Зарядим конденсатор от батареи и подключим его к катушке. В созданном нами контуре сразу же начнутся электромагнитные колебания (рис. 46). Разрядный ток конденсатора, проходя по катушке, создает вокруг нее магнитное доле. Это значит, что во время разряда конденсатора энергия его электрического поля переходит в энергию магнитного поля катушки, подобно тому как при колебаниях маятника или струны потенциальная энергия переходит в кинетическую.

По мере того как конденсатор разряжается, напряжение на его обкладках падает, а ток в контуре растет, и к тому моменту, когда конденсатор полностью разрядится, ток будет максимальным (амплитуда тока). Но и после окончания разряда конденсатора ток не прекратится – убывающее магнитное поле катушки будет поддерживать движение зарядов, и они вновь начнут накапливаться на обкладках конденсатора. При этом ток в контуре уменьшается, а напряжение на конденсаторе растет. Этот процесс обратного перехода энергии магнитного поля катушки в энергию электрического поля конденсатора несколько напоминает то, что происходит, когда маятник, проскочив среднюю точку, поднимается вверх.

К моменту, когда ток в контуре прекратится и магнитное поле катушки исчезнет, конденсатор окажется заряженным до максимального (амплитудного) напряжения обратной полярности. Последнее означает,что на той обкладке, где раньше были положительные заряды, теперь будут отрицательные, и наоборот. Поэтому, когда вновь начнется разряд конденсатора (а это произойдет немедленно после того, как он полностью зарядится), то в цепи пойдет ток обратного направления.

Периодически повторяющийся обмен энергией между конденсатором и катушкой и представляет собой электромагнитные колебания в контуре. В процессе этих колебаний в контуре протекает переменный ток (то есть изменяется не только величина, но и направление тока), а на конденсаторе действует переменное напряжение (то есть изменяется не только величина напряжения, но и полярность зарядов, накапливающихся на обкладках). Одно из направлений напряжения тока условно называют положительным, а противоположное направление – отрицательным.

Наблюдая за изменениями напряжения или тока, можно построить график электромагнитных колебаний в контуре (рис. 46), подобно тому как мы строили график механических колебаний маятника (рис. 39). На графике значения положительного тока или напряжения откладывают выше горизонтальной оси, а отрицательного – ниже этой оси. Ту половину периода, когда ток протекает в положительном направлении, часто называют положительным полупериодом тока, а другую половину – отрицательным полупериодом тока. Можно говорить также и о положительном и отрицательном полупериоде напряжения.

Хочется еще раз подчеркнуть, что слова «положительный» и «отрицательный» мы используем совершенно условно, лишь для того чтобы отличить два противоположных направления тока.

Электромагнитные колебания, с которыми мы познакомились, называют свободными или собственными колебаниями. Они возникают всякий раз, когда мы передаем контуру некоторый запас энергии, а затем даем возможность конденсатору и катушке свободно обмениваться этой энергией. Частота свободных колебаний (то есть частота переменного напряжения и тока в контуре) зависит от того, насколько быстро конденсатор и катушка могут накапливать и отдавать энергию. Это, в свою очередь, зависит от индуктивности _Lк и емкости С_к контура, подобно тому, как частота колебаний струны зависит от ее массы и упругости. Чем больше индуктивность L катушки, тем больше времени нужно, чтобы создать в ней магнитное поле, и тем дольше это магнитное поле сможет поддерживать ток в цепи. Чем больше емкость С конденсатора, тем дольше он будет разряжаться и тем больше времени понадобится, чтобы этот конденсатор перезарядить. Таким образом, чем больше _Lк и С_к контура, тем медленнее происходят в нем электромагнитные колебания, тем ниже их частота. Зависимость частоты f_о свободных колебаний от L_к и С_к контура выражается простой формулой, которая является одной из основных формул радиотехники:

Смысл этой формулы предельно прост: для того чтобы увеличить частоту собственных колебаний f, нужно уменьшить индуктивность L_к или емкость С_к контура; чтобы уменьшить f, индуктивность и емкость нужно увеличить (рис 47).

Из формулы для частоты можно легко вывести (мы это уже делали с формулой закона Ома) расчетные формулы для определения одного из параметров контура L_к или С_к при заданной частоте _f0 и известном втором параметре. Удобные для практических расчетов формулы приведены на листах 73, 74 и 75.